原文:R.Knott,数学科普作家。
译者:汪洋,遇见数学翻译组成员。
斐波纳契(Fibonacci)中世纪欧洲比萨共和国的意大利数学家,被认为是当时“ 最有才华的西方数学家”。不过我们现在来这样称呼他,可能会让他本人列奥纳多·皮萨诺(Leonardo Pisano)感到错愕。同样让他感到惊讶的是,最让世人津津乐道是以他命名的这个斐波那契数列:0,1,1,2,3,5,8,13……,而并非本人更伟大的数学成就——将阿拉伯数字和乘数的位值表示法系统引入了欧洲。

Leonardo Bonacci, Leonardo Fibonacci,1175年-1250年
神圣的罗马帝国给欧洲留下了罗马数字系统,直至今日在很多电影中的版权声名里,我们仍然可以看到"2013年是 MMXIII "这样的表述。罗马数字直到公元13世纪中叶才被阿拉伯数字取代,列奥纳多·皮萨诺的著作《计算之书》(Liber Abaci),就是最早推荐用阿拉伯数字来取代罗马数字的西方书籍之一。
列奥纳多·皮萨诺出生于12世纪末意大利比萨城,所以人们又称他为比萨的列奥纳多。皮萨诺,在意大利语中表示他来自比萨城,正如曼彻斯特表示来自曼彻斯特一样。列奥纳多的父亲名叫古列尔莫·巴纳奇奥( Guglielmo Bonaccio)。几个世纪后,当学者们研究《计算之书》的手抄本时(因为它是在印刷术发明之前出版的),他们误解了书名的一部分-"filius Bonacci"(意思是Bonaccio之子)的缩写Fibonacci解读为他的姓氏,于是我们称道的大数学家”斐波那契”由此这个错误中流传至今了。
斐波那契(我们还是这样称呼他吧)在北非度过了他的童年,接受过摩尔人的教育,在巴尔巴里(阿尔及利亚),游历甚广,后来被派往埃及、叙利亚、希腊、西西里和普罗旺斯出差。公元1200年,他回到比萨后,利用在旅行中所学到的知识撰写了《计算之书》(出版于1202年)。就是在这本书里他把印度-阿拉伯数字系统引入到了当时的拉丁语世界中。在该书的第一部分第一章开始部分写道:
"这是印度人的九个数字:9 8 7 6 5 4 3 2 1。用这9个数字,再加上符号0(在阿拉伯语中称为zephiroum),我们就能将任何数字都可以像下面那样书写出来"。

当时的意大利是由独立的小城邦和地区组成的,这导致了人们使用多个度量和货币系统。而当商人在不同的系统之间进行交易时,被迫要从一个系统换算到另一个系统,而落后的罗马数字计算方式更是严重抑制了商业行为。斐波那契为这些商人编写了《计算之书》,其中就涉及到大量的实际问题,并举例说明,与笨拙的罗马数字相比,这套新的数字系统可以多么简单、高效地进行商业和数学计算。透过斐波那契的这本书将十进制数字影响传播开来是他最伟大的数学成就。然而,本人却是因为《计算之书》中列举的斐波那契数列被世人所熟知的。
斐波那契的兔子问题
斐波那契在《计算之书》中研究的一个数学问题是关于兔子在理想环境下繁殖的速度。假设一对新生的兔子,一只公的,一只母的,被放进田里豢养。兔子可以在一个月大的时候交配,这样在第二个月的月底,雌性兔子就能生产出另一对兔子。假设兔子永远不会死,从第二个月开始,雌兔每个月都会生一对新的兔子(一只雄的,一只雌的)。斐波那契提出的问题是。一年后总共会有多少对兔子?
· 在第一个月末,它们交配,但仍然只有一对。
· 在第二个月末,雌兔生了一对新的兔宝宝,所以现在共有2对兔子。
· 在第三个月末,原来的雌性产生了第二对,总共生产了3对。
· 在第四个月末,原来的雌性又生产了一双新的,两个月前出生的第二代雌性也生产了她的第一对,现在共有五对兔子。
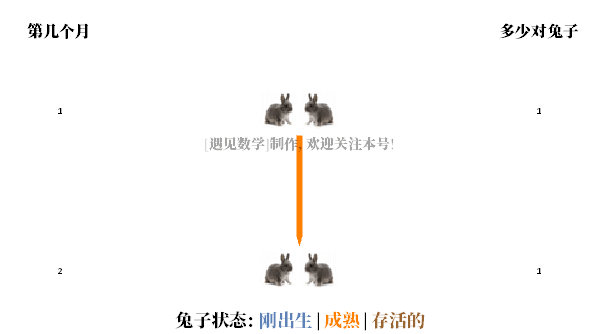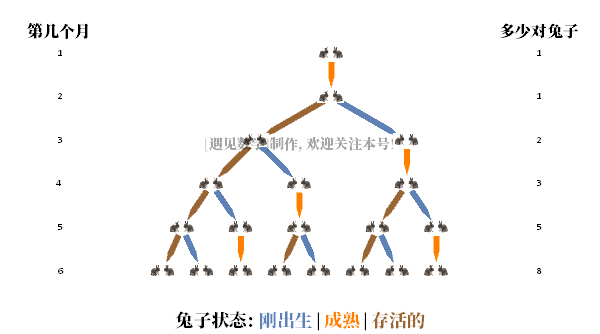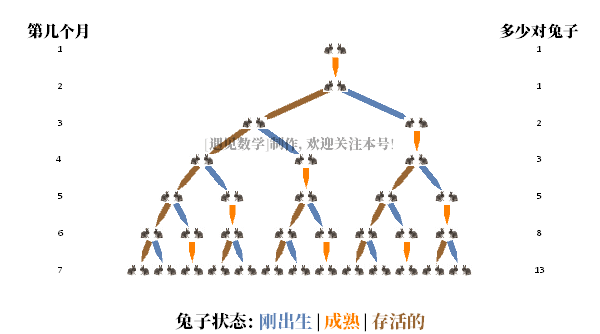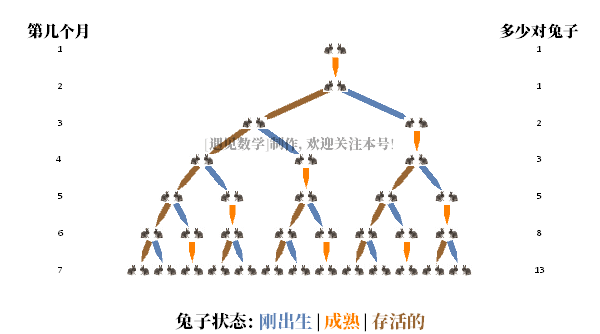
现在假设一下,n个月后有 x_n 对兔子。则 n+1个月将有的兔子数,是 x_n 对兔子,(兔子永远不会死)加上新出生的一对数。但是新的一对只出生在至少一个月大的时候,所以会有 x_(n-1) 对新兔子。所以我们有
这只是产生斐波那契数列的规则:最后两项相加得到下一项。接下来,你会发现在12个月之后,将会有233对兔子。
其实以蜜蜂为例更好
兔子的问题显然是人为设立出来的,但斐波那契数列也确实出现在大自然实际种群中,而蜜蜂就是其中一个实例。在蜂群中,有一种特殊的雌性叫做蜂王。其他雌性都是工蜂,而工蜂不会产卵。另外的雄性蜜蜂并不工作,被称为雄蜂。
雄蜂是由蜂王的未受精卵子产生的,所以说它只有母亲而没有父亲。而所有的雌性都是在蜂王和一只雄性交配的时候产生的。因此,雌性蜜蜂有父母,一个雄性和一个雌性,而雄蜂只有一个母亲,一个雌性。
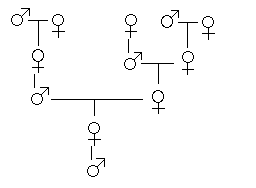
现在让我们看看上面雄蜂的家谱从下往上来看,就会再一次看到其中的斐波那契数列了吧.
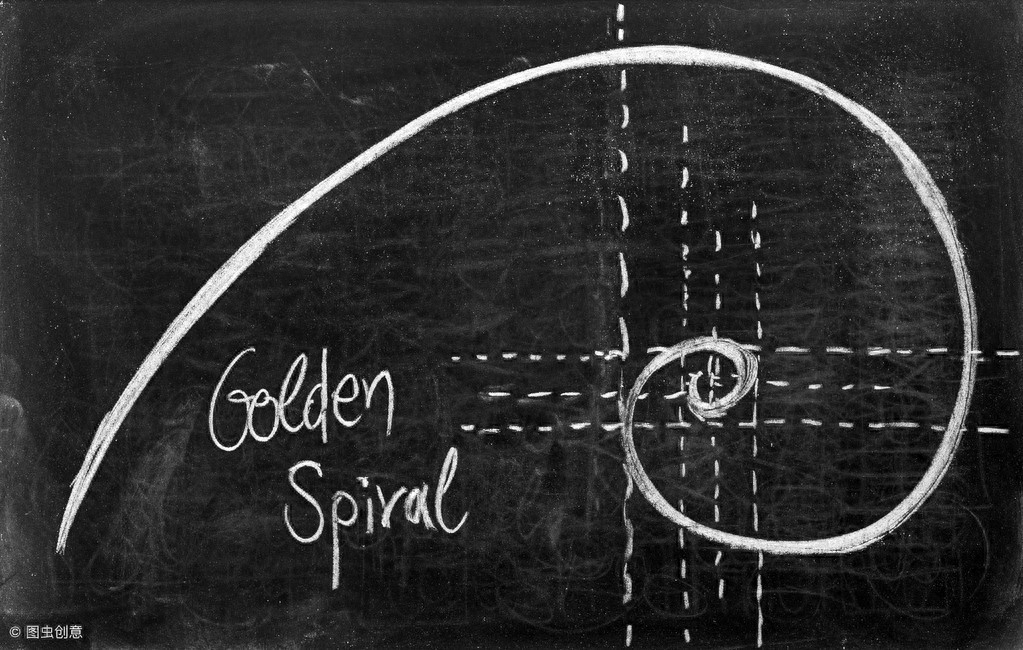
螺旋与贝壳

蜜蜂种群并不是自然界中唯一出现斐波那契数的地方,它们也以美丽的贝壳螺旋形状出现。我们可以看下面的动画,从两个大小为1的小正方形开始。在这两个小正方形上面画一个大小为2的正方形(=1+1)。我们现在可以画一个新的正方形-同时紧贴一个单位正方形和第二个新正方形的边的,所以边有3个单位长;然后另一个同时紧贴2个正方形和3个正方形(它有5个单位的边)。我们可以继续在图片周围添加正方形,每一个新的正方形都有一个边,其长度与最近两个正方形的边之和一样长。这组矩形的边长是两个相邻的斐波那契数,我们称之为黄金矩形.

如果我们现在每个正方形上画一个四分之一的圆,我们就可以画出一条螺旋线。准确来讲,这条螺旋不是真正的数学螺旋线(因为它是由圆弧线段组成的,且半径不会越变越小),但它可以很好的近似于经常出现在自然界中的螺旋形状,比如蜗牛和贝壳。在下面的图像中,一只海洋贝壳的横截面显示了贝壳的螺旋曲线。

斐波那契数列也出现在植物的花瓣、萼片中。有些植物也按这种方式生长开来,比如雏菊可以有34,55,甚至多达89瓣!还有就是一个特别神奇、美丽的排列是花蕾中的螺旋线。下一次当你看到向日葵时,仔细观察花盘中的种子排列,会发现两组螺旋线,一组顺时针向右,一组逆时针向左,并且彼此镶嵌,按照这种方式排列生长。

观察上面这幅向日葵图片的边缘,如果你数一数,当你向外走的时候,种子的曲线向左螺旋,就会有55个螺旋。在同一点上,有34个螺旋种子螺旋向右螺旋。再往中间一点,你可以数到左边34个螺旋,右边21个螺旋。在斐波那契数列中,数字对(向左弯曲和向右弯曲的螺旋数)总是相邻(如下图所示)。
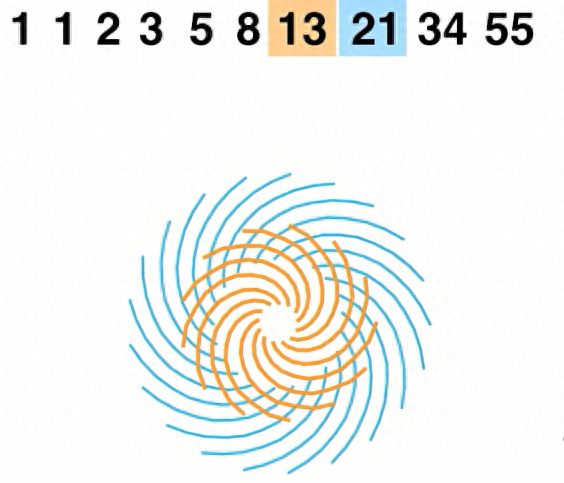
自然界中的许多种子和花蕾也是如此。原因似乎是这种结构形成了种子的最佳布局,因此,无论种子有多大,它们在任何阶段都是均匀分布的,所有种子大小相同,中心不拥挤,边缘不太稀疏,花盘也最为坚固。
大自然似乎用相同的模式把花瓣围绕在花的边缘,把叶子分布在茎周围。更重要的是,在植物整个持续生长的过程中,都保持着这种结构!那么,植物是如何做到保持这个的最优方式呢?
物竞天择的黄金生长
植物学家已经证明,植物都是由其顶端被称作分生组织的细胞分裂生长而成的。在每个分枝或小枝的末端有一个独立的分生组织,有此处形成新的细胞。一旦形成,它们的大小就会增长,但是新的细胞只会在这样的生长点破壁而出。细胞在绕着茎干,向外奋力长出。而且,这些细胞呈螺旋状生长,就像分生组织以一个角度旋转,产生一个新的细胞,以同样的角度再次旋转,再产生一个新的细胞,如此下去。这些细胞可能是新的种子,新的花瓣,新的枝条。

这里的叶子是依次编号的,每一个都是前一个顺时针旋转(222.5°)的0.618圈。
令人惊奇的是,无论植物有多大,这样一个固定的旋转角度都能产生最优的布局设计。早在上个世纪就有人推测,按照这个角度总能产生均匀填满平面空间,但直到1993年才由和两个法国数学家从数学上得以证明。在新种子(或叶子、花瓣等)破壁而出之前,这样做0.618圈旋转就会产生最佳的种子布局,但是这个神奇的数字0.618又是从何而来的呢?

黄金比例 φ
如果我们取斐波那契数列中两个连续数的比率,除以前面的数,我们会得到以下数列:

如果你绘制出这些值的图表,你会发现它们似乎趋向于一个极限,我们称之为黄金比例(亦称黄金数和黄金分割).
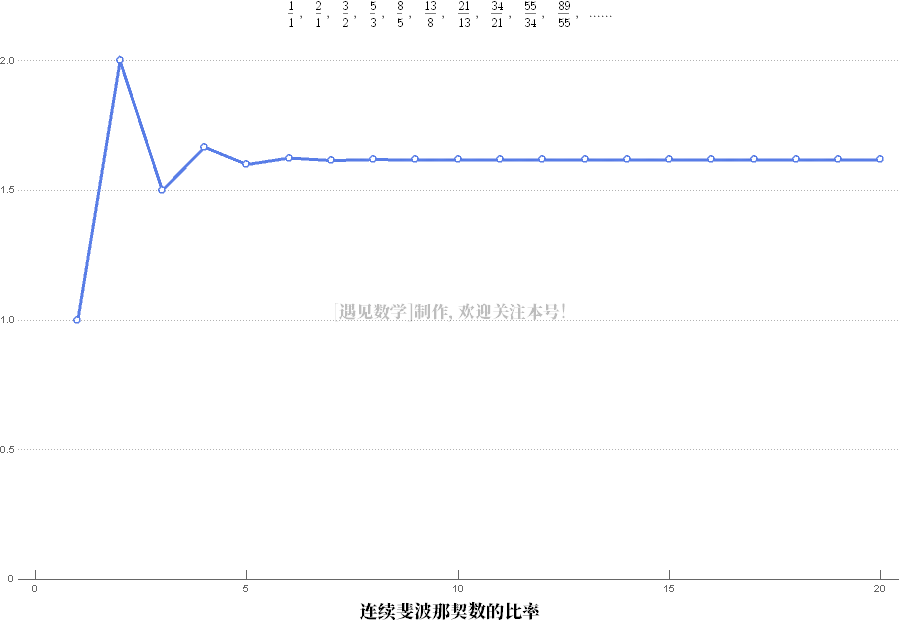
连续斐波那契项的比率准确值是 (√5 + 1)/2 (约1.618034),通常用希腊字母Phi(大写的希腊字母Φ)表示。Phi的小数部分用小写的phi(希腊字母:φ)表示, 准确值为 (√5 - 1)/2 , 约等于0.618034。这个φ与许多植物种子中螺旋线的数量以及叶序的排列更为密切,所以我们也会在很多种的植物中看到φ的身影。
数值Phi是无理数,同样phi也是无理数,就是说它们不能写成一个简单的分数形式。让我们看看,如果植物的分生组织按一些更简单的数字旋转,例如1/2,会发生什么。经过旋转两圈后,我们又回到了第一颗种子的方向。随着时间的推移,随着新种子在中心不断长出,每转动半圈就推动之前的种子往两个生长的方向辐射出去,而余留上下平面空间。
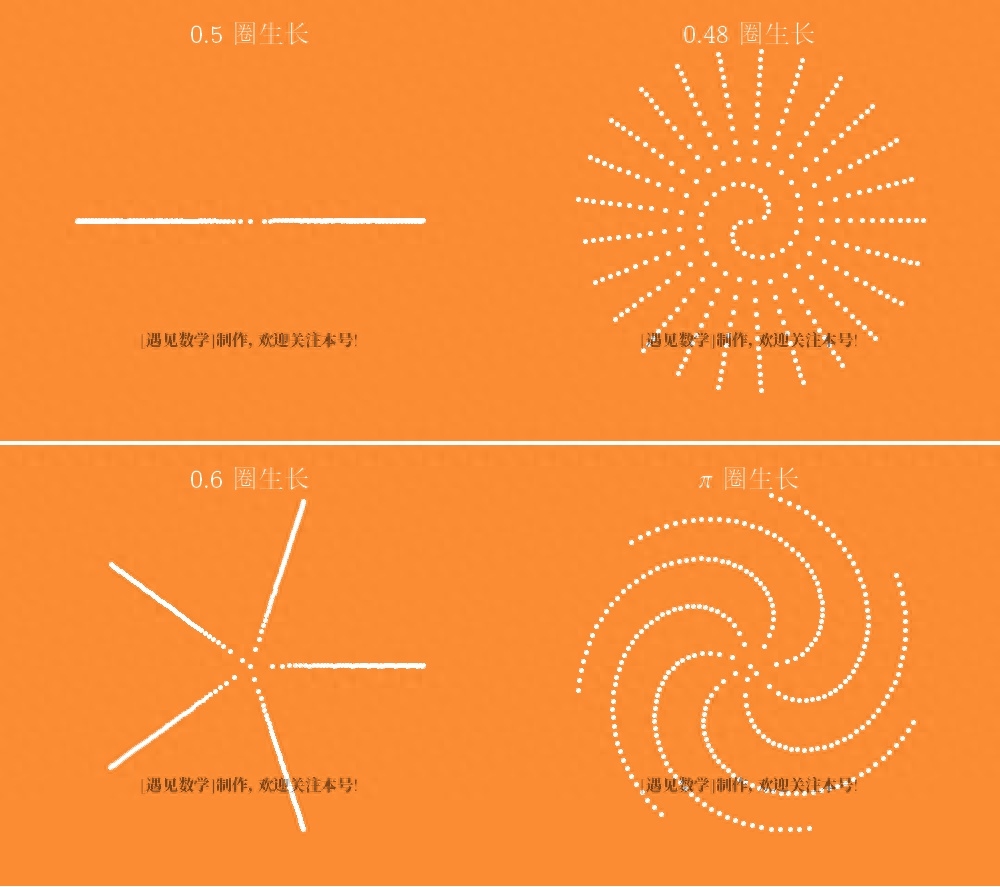
类似图案发生在按照其他数值进行旋转的情形:如果种子按照上面几个螺旋线的路径不断分裂长出,那在它们之间就会留下很大的空间(螺旋线数目就是这个比例的分母)。因此,螺旋线数的最佳值将是一个无理数。但不是任何无理的数都可以。例如,按照 π 值生长似乎有七条螺旋线,这是因为 22/7 是π的一个很好的有理逼近。
为了尽可能的利用空间,需要的是一个尽量不能被有理数所近似的无理数,这个结果就是Phi或phi,因为它们是所有无理数中"最不理性的"。这就是为什么Phi值的变化给出了植物种子和叶子的最佳布局。这也解释了为什么斐波那契数列会出现在叶序和花盘的上螺旋生长线上——相邻斐波那契数的比率最终无限趋近于黄金比例。

那么植物是如何发现这个美丽且实用的数字φ呢?显然不是像斐波那契那样通过解数学计算得出的。而是植物在亿万年进化的过程中逐步演化停留在最合适自己生存的数字上。斐波那契所留下的遗产不仅闪烁在每株植物的花蕾之上,也是数学世界所绽放最耀眼魅力光芒中的一束。

发表评论