当我们想要比较两组数据是否有差异时,往往首先想到计算出两组数据的均值,从而比较两组数据的差异,然而这些参数只能反映样本的特征,不能直接反映总体的分布特征。单独使用这些参数比较两组数据是否有差异时往往会产生较大的误差,因此统计学家们常使用t检验来检验两组数据是否有差异。t检验(Student’s tese)主要适用于样本量较少,总体标准差σ未知的正态分布。T检验根据研究方法和性质的不同分为单样本t检验、配对样本t检验以及独立样本t检验,亦有在数据方差不齐时使用的t’检验,本文首先介绍比较常用的两独立样本t检验(Two-sample t-test)。
抽取县医院4月份骨科和妇产科住院病人各10人,统计他们的住院天数,如表-1所示,我们虽然可以通过直接观察数据或者计算平均数比较发现骨科病人的住院天数大于妇产科病人,但是这样并不能解释这种差异是否是由于抽样误差所造成的,因此我们需要使用更加科学的统计学方法进行分析。
表-1 骨科、妇产科病人住院天数
科室
病人住院天数
骨科
12
10
11
13
12
11
14
11
妇产科
这里首先,我们列出解题思路:
(1)建立检验假设,确定检验水准
H0:μ1=μ2,妇产科和骨科病人住院时间的总体均数相同
H1:μ1≠μ2,妇产科和骨科病人住院时间的总体均数不同
(2)计算检验统计量:这里我们使用SPSS统计分析软件对这组数据进行t检验,将统计数字导入SPSS后设定相应参数,得出如表-2、表-3所示结果,表-2中给出了两组病人住院天数的标准差、平均值等数据,表-3首先对两组数据进行了方差齐性检验,莱文方差等同性检验显示两组数据的P值为0.659,明显大于0.05的界限,表明可以认为两组数据方差齐,方差齐时使用表-3第一列t检验结果,可观察到t检验的P值小于0.001。
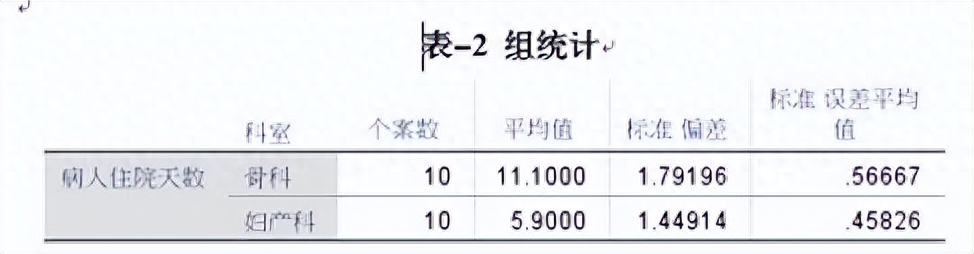
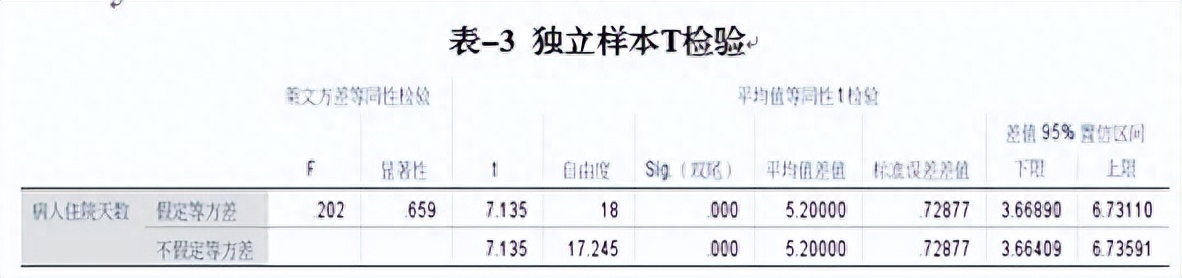
(3)根据P值,作出推断结论:两独立样本t检验的自由度为18,P<0.05,按照α=0.05的水平拒绝H0,接受H1,两组差异有统计学意义,可以认为骨科和妇产科病人的平均住院天数存在差异。
两组样本的整体分布符合t检验是使用两独立样本T检验的必要条件,除此之外,两组数据的总体方差σ1余σ2必须一致或相近,即两组数据必须有方差齐性(Homogeneity of variance),两组样本方差不齐时可以使用变换变量法,或采用t’检验或非参数检验方法进行分析。
【参考文献】
李康,贺贾.医学统计学(第六版)[M].人民卫生出版社,2013.62-63.
备注:本文章于2022年5月13日22:00使用paperyy进行查重,查重率21.8%,由于文章内容较少且涉及到一些常用统计学概念,故查重率稍高。

发表评论