
公共物品
37.1复习笔记
1离散数量的公共物品的提供
(1)模型假设
①假定某房间有两个人1和2,他们现在要决定是否购买某公共品。如果用ω1和ω2代表每个人的初始财富,g1和g2代表每个人对购买公共品作出的贡献,x1和x2表示剩下来用作私人消费的资金,每个人的预算方程为:
x1+g1=ω1
x2+g2=ω2
②假定公共品的成本为c美元,为了使公共品得到提供,应当有g1+g2≥c;
③消费者i的效用函数为ui(xi,G),他愿意为购买公共品支付的保留价格为ri,即ui(ωi-ri,1)=ui(ωi,0),这里i=1或2,G=0(没有公共品)或1(有公共品)。
(2)公共品的提供条件
如果购买公共品使两人的境况得到改善,就有:
u1(ω1,0)<u1(x1,1)
u2(ω2,0)<u2(x2,1)
运用保留价格r1和r2以及预算约束的定义,就有:
u1(ω1-r1,1)=u1(ω1,0)<u1(x1,1)=u1(ω1-g1,1)
u2(ω2-r2,1)=u2(ω2,0)<u2(x2,1)=u2(ω2-g2,1)
再由效用函数单调递增的特性,就有:
ω1-r1<ω1-g1
ω2-r2<ω2-g2
于是就有r1>g1,r2>g2,同时只有当r1+r2≥g1+g2≥c时,公共品才会被提供。
综上所述,可以得到公共品提供的必要条件:r1+r2>c。
(3)关于公共品提供条件的若干注释
①提供公共物品是否是一种帕累托改进仅取决于人们的支付意愿和公共物品的总成本。如果保留价格总和大于公共品的成本,那么肯定存在着某种支付方案,使两人拥有这种公共物品的境况比不拥有时的境况要好;
②提供公共物品是否是帕累托有效,还取决于初始的财富分配(ω1,ω2)。这是因为保留价格r1和r2一般是由财产分配决定的,某些财产分配完全有可能使r1+r2>c,而另一些财产分配则可能使r1+r2<c。
(4)消费者偏好为拟线性时公共物品的提供
此时消费者的效用函数有如下形式:
ui(xi,G)=xi+υi(G),i=1或2
为简化起见,再假定:
υ1(0)=υ2(0)=0
由于:υ1(ωi-ri,1)=ωi-ri+υi(1)=ωi=ui(ωi,0),从而得到:ri=υi(1)。
可见保留价格与财富数量无关,因而公共物品的最优供给将与财富无关。
(5)公共物品提供中搭便车的例子
假定每人有500美元的财富,每个人对公共品的评价是100美元,公共品的成本是150美元。由于保留价格的总和大于公共品的成本,所以,购买公共品是帕累托有效率的。如果两个人独立地决定是否购买公共品,就得到如下的收益矩阵:
这个博弈的占优策略均衡是两个参与人都不购买公共品,但帕累托有效的均衡却是其中一个人购买,而另一个人不购买。这里就出现了搭便车的情况,因为如果对方购买,不买总是己方的最优策略,但每个人都这样做的结果是大家都不购买,从而产生帕累托无效的结果。
2连续数量的公共物品的提供
(1)公共物品提供的萨缪尔森规则
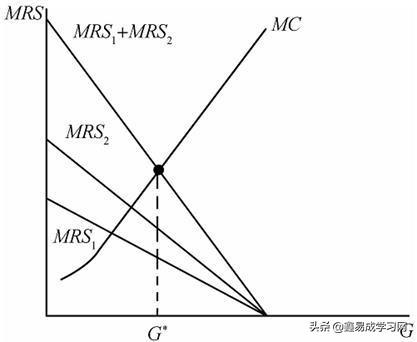
令x1和x2代表消费者的私人消费(这里私人消费品是计价物),G代表公共品的总数量,C(G)表示公共品的生产成本。那么公共物品提供的萨缪尔森规则就是:MRS1+MRS2=MC,即私人物品和公共物品之间的边际替代率之和等于公共物品的边际成本,如图37-1所示。
图37-1公共物品的有效供给
(2)对萨缪尔森规则的推导
帕累托有效配置是指在消费者2的效用水平不变的条件下使消费者1的效用水平尽可能大。如果把消费者2的效用固定在某一水平u_2上,消费者1的效用最大化问题就可以表述为:
x1+x2+C(G)=ω1+ω2
利用拉格朗日乘数法,可以得到:MRS1+MRS2=MC。
(3)对于萨缪尔森规则的解释
如果把边际替代率视为对额外一单位公共物品的边际支付意愿的衡量,那么,萨缪尔森规则就是说边际支付意愿相加之和必须等于多提供一单位公共物品的边际成本。
(4)公共物品和私人物品帕累托有效条件的区别
①就私人物品而言,每个人的边际替代率必须等于边际成本;就公共物品而言,边际替代率相加之和必须等于边际成本;
②在私人物品市场,每个人可以消费不同数量的私人物品,但他们对边际消费量的评价必定全部相同,否则他们要进行交换。在公共物品市场,每人的消费量必定相同,但他们对边际消费量的评价可以各不相同。
(5)拟线性偏好的公共物品提供数量
如果消费者的效用函数具有拟线性形式,即:ui(xi,G)=xi+vi(G),这里i=1或2,那么:
MRS1=v1′(G),MRS2=v2′(G);
根据萨缪尔森规则,有:v1′(G)+v2′(G)=MC(G),从而公共物品的有效数量与x1和x2无关,所以存在唯一的公共物品有效供给数量。
3公共品提供中的搭便车问题
(1)模型假设
x1表示行为人1的私人消费,g1表示他购买的公共物品的数量;x2表示行为人2的私人消费,g2表示他购买的公共物品的数量,G=g1+g2是公共物品的总量。公共物品的生产成本为C(G)≡G,第i个人的效用函数为ui(xi,g1+g2)=ui(xi,G),i=1或2。
(2)行为人1的最优决策
给定行为人1对行为人2购买的公共品数量的预期g_2,其最优决策为:
从而得到行为人1的反应函数:g1=f1(g_2)。
(3)行为人2的最优决策
类似于(2),行为人2的反应函数为:g2=f2(g_1)。
(4)市场均衡
当每个人的预期都等于对方的实际购买量时,市场达到均衡(纳什均衡),即:
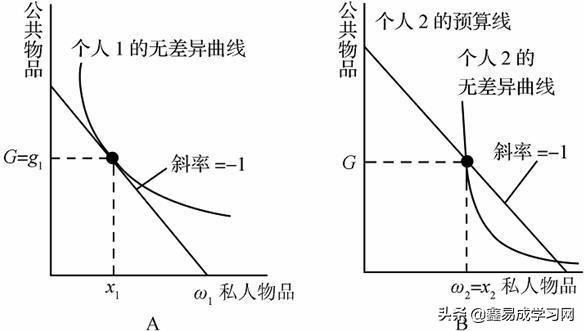
由于每个人至少可以消费对方提供的公共品数量,所以当达到均衡时,有可能出现这样一种情况,即:乙认为甲贡献的公共品的数量已完全足够,因而他不需要再作出任何贡献,从而出现了搭便车的现象,如图37-2所示。
图37-2公共品提供中的搭便车
(5)与私人物品的比较
对于私人品而言,完全竞争市场可以为其提供一种达到帕累托有效配置的途径,在这种市场上,每个消费者只需要关心自己的消费数量。这种分析的一个重要假定是一个人的消费不会影响到其他人,即不存在消费的外部效应,因此每个人都使自身的消费达到最优就足以形成全社会的最优。
但对于公共物品而言,情况有着很大差异。在这种情况中,由于每个人需要消费同样数量的公共物品,因此它们之间的效用是紧密相关的,在这种情况下,市场提供的公共品数量不大可能导致帕累托有效的结果。因此需要其他某种机制来确定公共品的有效供给。
4需求显示
(1)问题陈述
在路灯安装的例子中,假定安装路灯的成本已知,比如说为100美元。第i个人对路灯的评价用Vi表示。如果每人的评价之和大于或等于安装路灯的成本,那么提供路灯就是有效的。
假设在决定是否要安装路灯之前,每人要预先支付一笔金额Ci作为其分担的安装费用,然后再让每人表明他或她的评价Vi,从而得到每个人的净值ni=Vi-Ci,这样通过加总净值就能知道各人评价之和是否超过成本。但这样的决策机制有一个问题,即每个人都有夸大自己评价的倾向。
(2)格罗夫斯-克拉克机制
格罗夫斯-克拉克机制可以克服每个人都夸大自己评价的可能性,其内容如下:
①向每个行为人指派成本Ci,这是指每个决定提供公共物品的人必须支付的费用;
②要求每个人都表明有一个净值si,(这既可以是,也可以不是他或她的真实净值ni);
③如果所表明的净值之和是正数,公共物品就得到提供,如果是负数,就不会被提供;
④要求每个关键人物纳税,即如果第j个人的决策使本来决定提供公共物品改变为不提供公共物品,那么他所负担的税收(克拉克税)就将是:
如果第j个人把不提供公共物品的决策变为提供公共物品,那么他负担的税收将是:
(3)克拉克税存在的问题
①克拉克税仅适用于拟线性偏好。这是因为每个消费者并不知道他必须交纳的这笔影响他对公共物品的需求的税负的数额。公共物品存在唯一的最优化水平十分重要;
②克拉克税实际上不会导致帕累托有效的结果。这是因为尽管公共物品的数量会最优,但私人消费可能更大;
③最后一个问题涉及到克拉克税固有的平等与效率的抉择问题。
由于支付计划必须预先确定,一般会产生下述现象:某些人的境况将由于公共物品的供给而变坏,尽管所供给的这种公共物品可能是帕累托有效数量。认为提供公共物品是一种帕累托有效,就等于是说有某种支付计划会使每一个人的境况在有公共产品提供时将比无公共产品提供时要好得多。但这并不意味着任意一个支付计划都会使每一个人的境况变得较好一些。克拉克税就是要保证,如果有公共物品提供会使每个人的境况变好一些,那么就应供给这种公共物品。当然这不一定意味着每个人的境况真的会更好一些。
看书和学习是思想的经常营养,是思想的无穷发展。——冈察洛夫

发表评论